Longest Common Subsequence Java Implementation using Dynamic Programming

You will be given two sequences and you have to find the length of longest subsequence common to both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous.

For example, “androi”, “arsc”, “anidc”, “roidsc”, “acefg” etc… are subsequence of “androidsrc”. For a sequence of length N, it will have 2^N subsequence.

Examples
LCS for “AMNPQ” and “BMANPQ” is “MNPQ” of length 4.
LCS for “AWNNDROMIDSPRCK” and “AYNDLROQIDZSRCM” is “ANDROIDSRC” of length 10.

LCS (Longest Common Subsequence) is typical example of Dynamic Programming. It satisfies both requirements of DP. It has got Optimal Substructure as well as Overlapping Sub-problems property.

Lets consider two input sequences Seq1[0..N-1] and Seq2[0..M-1] of length N and M respectively. Let LCS(Seq1[0..N-1],Seq2[0..M-1]) be function that gives length of longest common subsequence.

While selecting for longest common subsequence from Seq1 and Seq2, we will process in two ways for index i in Seq1 and j in Seq2.

If there is a match in Seq1 and Seq2, we increment LCS length by 1 and process Seq[1..N-1] and Seq[1..M-1} i.e. LCS(Seq1[i..N-1],Seq2[j..M-1]) = 1 + LCS(Seq1[i+1..N-1],Seq2[j+1..M-1]) (if Seq1[i] == Seq2[j])

In case of mismatch we can either select from Seq1 or Seq2 which gives us two ways. Since we have to determine longest common sequence, we need maximum of these two. i.e. LCS(Seq1[i..N-1],Seq2[j..M-1]) = Max(LCS(Seq1[i+1..N-1],Seq2[j..M-1]), LCS(Seq1[i..N-1],Seq2[j+1..M-1])) (if Seq1[i] != Seq2[j])

We can observe from above LCS calculation that it has optimal substructure.

Lets take example of Seq1 = “AMNPQ” and Seq2 = “BMANPQ”

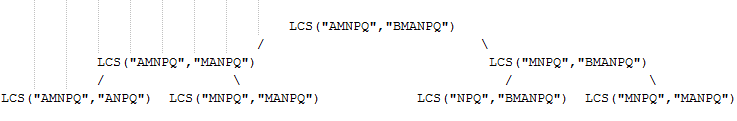
If you observe in above incomplete recursion tree, we are calculating LCS(“MNPQ”,”MANPQ”) twice. It satisfies overlapping sub-problems as well.

For computing LCS length, we will be constructing lcs_table[N+1][M+1] to avoid recalculation for sub-problems. Lets build lcs_table for above example. Initialize first row and first column to zero.

		B	M	A	N	P	Q
	0	0	0	0	0	0	0
A	0
M	0
N	0
P	0
Q	0

Now let’s fill above table as explained before

lcs_table[i][j] = 1+lcs_table[i-1][j-1]   (if Seq1[i-1] == Seq2[j-1])

lcs_table[i][j] = Max(lcs_table[i-1][j], lcs_table[i][j-1]) (if Seq1[i-1] != Seq2[j-1])

After filling table, your final values will be

	B	M	A	N	P	Q
	0	0	0	0	0	0	0
A	0	0	0	1	1	1	1
M	0	0	1	1	1	1	1
N	0	1	1	1	2	2	2
P	0	1	1	1	2	3	3
Q	0	1	1	1	2	3	4

Thats’ all, lcs_table[N][M] is your result value. In this case, MNPQ of length 4.

Java code to compute LCS length.